Введение в OpenSceneGraph: Обход графа сцены. Ноды трансформации
Типичный алгоритм обхода графа сцены состоит из следующих шагов:
- Начинаем с произвольного узла (например с корневого узла)
- Перемещение вниз (или вверх) по графу сцены рекурсивно до достижения листового узла или узла, не имеющего дочерних узлов
- Откат к самому последнему узлу, на котором не завершается поиск и повторение шагов 1 и 2. Это называется поиском в грубину по графу сцены.
Во время обхода графа к узлам сцены применяются различные операции обновления и рендеринга. Существует несколько типов обхода, преследующих различные цели:
- Обход с целью обработки событий ввода вывода от мыши и клавиатуры и других пользовательских устройств ввода
- Обход с целью обновления узлов, позволяющий пользовательскому приложению модифицировать граф, например устанавливать совйства узлам и геометрии, применять к нодым новую функциональность, выполнение обратных вызовов (callbacks) и так далее.
- Обход с целью отсечения невыидимых и неотображаемых узлов и выод оптимизированного дерева во внутрений список рендеринга.
- Обход отрисовки (рендеринга) - выполнение низкоуровневых инструкций OpenGL для отображения сцены на экране. Следует помнить, что процесс рендеренга никах не коррелируется с текущим состоянием графа сцены, а выполняется по списку, сгенерированного после прохода отсечения.
Если говорить в целом, то эти обходы выполняются за время отрисовки кадра один за другим. Однако, в многопроцессорных и многоядерных системах OSG может выполнять эти проходы параллельно. Для реализации обхода графа может использоваться паттерн Visitor, о чем мы поговорим чуть попозже.
Ноды трансформации
Узлы osg::Group не могут делать никаких преобразований, кроме возможности перехода к своим дочерним узлам. Для пространственного перемещения геометрии OSG предоставляет класс osg::Transform. Этот класс является наследником класса osg::Group, но и сам является абстрактным - на практике вместо него применяются его наследники, реализующие различные пространственные преобразования геометрии. При обходе графа сцены узел osg::Transform добавляет свое преобразование в текущую матрицу преобразования OpenGL. Это эквивалентно перемножению матриц преобразования OpenGL, выполняемое командой glMultMatrix()
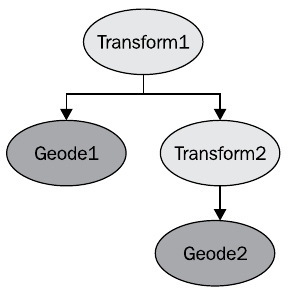
Этот пример графа сцены можно транслировать в следующий кода на OpenGL
glPushMatrix();
glMultMatrix( matrixOfTransform1 );
renderGeode1();
glPushMatrix();
glMultMatrix( matrixOfTransform2 );
renderGeode2();
glPopMatrix();
glPopMatrix();
Можно стказать, что положение Geode1 задается в системе координат Transform1, а положение Geode2 задается в системе координат Transform2, смещенной относительно Transform1. При этом в OSG можно включить позиционирование в абсолютных координатах, что приведет к поведению объекта, эквивалентному результату команды glGlobalMatrix() OpenGL
transformNode->setReferenceFrame( osg::Transform::ABSOLUTE_RF );
Можно переключится обратно в режим позиционирования относительными координатами
transformNode->setReferenceFrame( osg::Transform::RELATIVE_RF );
Понятие о матрице преобразования координат
Тип osg::Matrix это базовый тип OSG не управляемый умными указателями. Он предоставляет интерфейс к операциями над матрицами размерности 4х4, описывающими преобразование координат, такин как перемещение, поворот, масштабирование и вычистение проекций. Матрица может быть задана явно
osg::Matrix mat(1.0f, 0.0f, 0.0f, 0.0f,
0.0f, 1.0f, 0.0f, 0.0f,
0.0f, 0.0f, 1.0f, 0.0f,
0.0f, 0.0f, 0.0f, 1.0f ); // Единичная матрица 4х4
Класс osg::Matrix предоставляет следующие публичные методы
- postMult() и operator* () - умножение справа текущей матрицы на матрицу или вектор, переданные в качестве параметра. Метод preMult() выполняет умножение слева.
- makeTranslate(), makeRotate() и makeScale() - сбрасывают текущую матрицу и создают матрицу 4х4 описывающую перемещение, вращение и масштабирование. их статические версии translate(), rotate() и scale() могут быть использованы для сосздания матричного объекта со специфическими параметрами.
- invert() - вычисление матрицы обратной текущей. Его статическая версия inverse() принимает в качестве параметра матрицу и возвращает новую матрицу, обратную данной.
OSG понимает матрицы как матрицы строк, а векторы как строки, поэтому для применения к вектору матричного преобразования следует поступать так
osg::Matrix mat = …;
osg::Vec3 vec = …;
osg::Vec3 resultVec = vec * mat;
Порядок матричных операций легко понять, посмотрев как перемножаются матрицы для получения эквивалетного преобразования
osg::Matrix mat1 = osg::Matrix::scale(sx, sy, sz);
osg::Matrix mat2 = osg::Matrix::translate(x, y, z);
osg::Matrix resultMat = mat1 * mat2;
Разработчик должен читать процесс трансформации слева направо. То есть, в описанном фрагменте кода сначала происходит масштабирование вектора, а затем его перемещение.
osg::Matrixf содержит элементы типа float.
Применение класса MatrixTransform
Применим полученные теоретические знания на практике, загрузив две модели самолета в разные точки сцены.
main.h
#ifndef MAIN_H
#define MAIN_H
#include <osg/MatrixTransform>
#include <osgDB/ReadFile>
#include <osgViewer/Viewer>
#endif
main.cpp
#include "main.h"
int main(int argc, char *argv[])
{
(void) argc; (void) argv;
osg::ref_ptr<osg::Node> model = osgDB::readNodeFile("../data/cessna.osg");
osg::ref_ptr<osg::MatrixTransform> transform1 = new osg::MatrixTransform;
transform1->setMatrix(osg::Matrix::translate(-25.0, 0.0, 0.0));
transform1->addChild(model.get());
osg::ref_ptr<osg::MatrixTransform> transform2 = new osg::MatrixTransform;
transform2->setMatrix(osg::Matrix::translate(25.0, 0.0, 0.0));
transform2->addChild(model.get());
osg::ref_ptr<osg::Group> root = new osg::Group;
root->addChild(transform1.get());
root->addChild(transform2.get());
osgViewer::Viewer viewer;
viewer.setSceneData(root.get());
return viewer.run();
}
Пример, на самом деле довольно тривиален. Загружаем модель самолета из файла
osg::ref_ptr<osg::Node> model = osgDB::readNodeFile("../data/cessna.osg");
Создаем ноду трансформации
osg::ref_ptr<osg::MatrixTransform> transform1 = new osg::MatrixTransform;
Устанавливаем в качестве матрицы преобразования перемещение модели по оси X на 25 единиц влево
transform1->setMatrix(osg::Matrix::translate(-25.0, 0.0, 0.0));
Задаем для ноды трансформации нашу модель в качестве дочернего узла
transform1->addChild(model.get());
Аналогично поступаем и со второй трансформацией, но в качестве матрица задаем перемещение вправо на 25 единиц
osg::ref_ptr<osg::MatrixTransform> transform2 = new osg::MatrixTransform;
transform2->setMatrix(osg::Matrix::translate(25.0, 0.0, 0.0));
transform2->addChild(model.get());
Создаем корневую ноду и в качестве дочених узлов для неё задаем трансформационные ноды transform1 и transform2
osg::ref_ptr<osg::Group> root = new osg::Group;
root->addChild(transform1.get());
root->addChild(transform2.get());
Содаем вьювер и в качестве данных сцены передаем ему корневую ноду
osgViewer::Viewer viewer;
viewer.setSceneData(root.get());
Запуск программы дает такую картинку

Структура графа сцены в этом примере такова
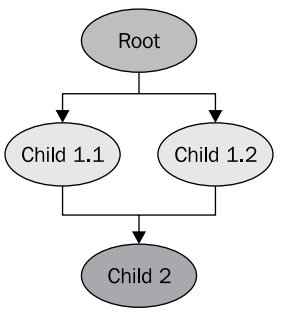
Нас не должен смущать тот факт, что ноды трансформации (Child 1.1 и Child 1.2) ссылаются на один и тот же дочерний объект модели самолета (Child 2). Это штатный механизм OSG, когда один дочерний узел графа сцены модет иметь несколько родительских узлов. Таким образом на не обязательно хранить в памяти два экземпляра модели, чтобы получить в сцене два одинаковых самолета. Такой механиз позволяет очень эффективно распределять память в приложении. Модель не будет удалена из памяти, пока на неё ссылается, как на дочернюю, хотя бы одна нода.
По своему действию класс osg::MatrixTransform эквивалентен командам OpenGL glMultMatrix() и glLoadMatrix(), реализует все виды пространственных преобразований, но сложен в использованию из-за необходимости вычислять матрицу преобразования.
Класс osg::PositionAttitudeTransform работает как функции OpenGL glTranslate(), glScale(), glRotate(). Он предоставляет публичные методы для преобразования дочерних узлов:
- setPosition() - переместить узел в данную точку пространства, зававаемую параметром osg::Vec3
- setScale() - масштабировать объект по осям координат. Коэффиценты масштабирования по соответствующим осям задаются параметром типа osg::Vec3
- setAttitude() - задать пространственную ориентацию объекта. В качестве прараметра принимает кватернион преобразования поворота osg::Quat, конструктор которого имеет несколько перегрузок, позволяющих задавать кватернион как непосредственно (покомпонентно), так и, например, через углы Эйлера osg::Quat(xAngle, osg::X_AXIS, yAngle, osg::Y_AXIS, zAngle, osg::Z_AXIS) (углы задаются в радианах!)